The circle of fifths is an incredibly helpful tool to help you keep track of which keys have which sharps or flats! It also helps you start to find connections between chords in music. All of the keys are related in some way, and going through the circle of fifths is a common way composers move between harmonies.
“Ok, that’s great. But how does it work? And how does it help me?”
Luckily, there are 12 Major and 12 Minor keys, and they come in pairs according to the number of sharps and flats. I say luckily, because this means you can read the circle of fifths similarly to how you read a clock. (You just might need a little more information to get started.)
At the very top, you find C Major and A Minor – the keys with 0 sharps and 0 flats. Moving clockwise through the circle of fifths, the notes ascend by a fifth, and you raise one note by a half-step for each subsequent key. Moving counterclockwise through the circle of fifths, the notes descend by a fifth, and you lower one note by a half-step for each subsequent key.
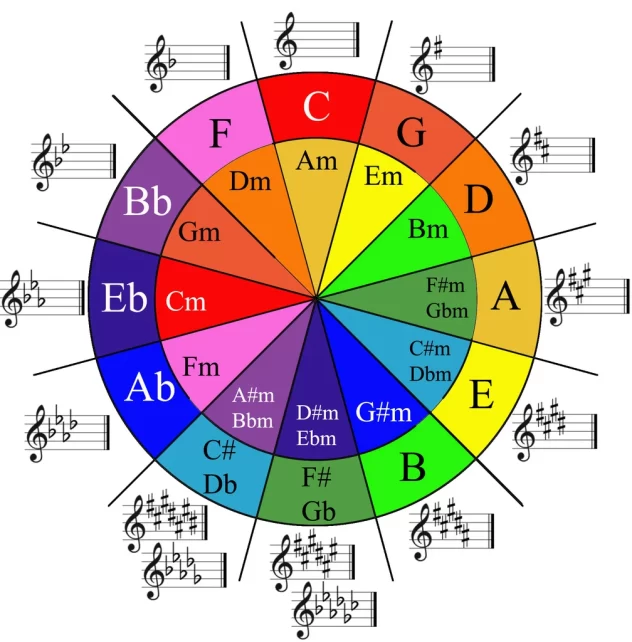
It is easy to keep track of the sharps and flats, because you can think of it a bit like a scavenger hunt. You collect one sharp or flat per position on the circle of fifths, and you keep it until it switches from sharps to flats or vice versa. For example, the keys with one sharp have F#, then the keys with two sharps add C# to the F#, and the keys with three sharps add G# to those, and so on. It’s systematic and simple – easy peasy!
Tricks to remember
It’s great to have the circle of fifths for reference, but in the end, you’re going to want to learn all of this by memory so that you can figure out everything about a key without referring to the diagram.
Start with the names of the keys
Start by trying to memorize the order of keys forwards and backwards. I like to visualize the 5ths on the piano to help me find my way. Going clockwise from C through the major keys, we have C, G, D, A, E, B, F#/Gb, C#/Db, Ab, Eb, Bb, F. Going clockwise from A through the minor keys, we have a, e, b, f#, c#, g#/ab, d#/eb, bb, f, c, g, d.
Notice that you don’t need to memorize an entirely different pattern for the minor keys. It’s actually the same pattern as the major keys, just starting from the fourth position. A few of the names are different, just because we would never refer to certain keys with sharps instead of flats or vice versa.
For example, F# Minor wouldn’t make much sense as Gb Minor. Gb Minor would have double flats (such as b double flat) as part of the key signature – that’s a mess that nobody wants to deal with! But once you get the hang of the order of the fifths, keeping track of the exceptions to the rule becomes quite easy.
Then the sharps/flats
Once you have mastered the order of the keys, you can start to hone in on which keys have which sharps and flats. Some of them you probably know well, like F Major, C Major, G Major, and D Major, but others are perhaps a bit hazy (I’m looking at you Eb Minor.)
One trick that can help is that the sharps and flats also appear in the order of fifths. The first sharp is F#, then comes C#, then G#, D#, A#, E#, and B#.
But what do you do once you’ve finished the sharps? The easiest option is to go back to C Major (no sharps or flats) and move counterclockwise, adding one flat at a time. Then, the first flat is Bb, then Eb, Ab, Db, Gb, Cb, and finally Fb. (Yes, Cb and Fb really exist. No, we don’t see them very often.)
For the purposes of showing the continuity of the circle of fifths, I do want to give an additional example. Once you have collected all of the sharps (F#, C#, G#, D#, A#, E#, B#), you can convert all of them to their enharmonic names (basically, the black keys become flats, and the white keys are given their “normal” names). This goes as follows:
F# → Gb
C# → Db
G# → Ab
D# → Eb
A# → Bb
E# → F
B# → C
That gives us the following collection of flats: Gb, Db, Ab, Eb, Bb. F and C are already naturals. To continue clockwise through the circle of fifths, the next note that is raised a half-step is Gb – to become G natural, leaving you with four flats. Then Db is raised to D, leaving you with three flats, Ab is raised to A, Eb is raised to E, and finally we raise Bb to B to return back to C Major. This method is perhaps less straightforward to follow, but it’s a nice way to understand how the circle of fifths really…goes full circle. (Sorry, the pun was just too easy.)
One last trick
In major keys, the new tone that is altered (going clockwise through the circle) is always the seventh scale degree. It’s the last note ascending, or the first note descending, however you want to remember it.
In minor keys, the new tone that is altered (going clockwise through the circle) is always the second scale degree.
How do you know which is the newest sharp or flat? Sharps and flats in time signatures always appear in order, so the newest is always the farthest to the right.
Have more specific questions about the circle of fifths? Or anything music theory related? Send me an email at robyn@pianowithrobyn.com, and I’m happy to help!

0 Comments